Research

My research interests are broad and span different topics in Computational Science, Parallel and High Performance Computing, Electrokinetics and Electrohydrodynamics, and Soft Matter Physics. In particular, I enjoy collaborating with researchers with various backgrounds from Physics, Applied Mathematics, and Computer Science. Below is a brief description of my past and present research. For a complete list of my publications please visit here.

Parallel Computing on Quadtree and Octree Grids

Despite continued trend in increasing computational power and cheaper computer memory, many physical and engineering problems are still too computationally expensive to run on a “typical” computer. Normally, such problems necessitate the use of parallel computing. However, for many multi-scale problems, a simple brute-force approach is not enough, specially in 3D where the “curse of dimensionality” quickly overwhelms available computational resources.

Fortunately, for many multi-scale problems, the separation of scales suggests that computational resources may be allocated more efficiently by using grid adaption. Tree-based adaptive grids, i.e. Quadtrees in 2D and Octrees in 3D, offer an elegant and efficient approach for automatic and dynamic grid adaption. A central theme of my research is designing computational methods for solution of PDEs on these grids. I am also interested in combining parallel computing and dynamic grid adaptation. Unlike regular grids, which are trivial to parallelize, the tree data structure in Quadtree and Octree grids must first be linearized and then dynamically partitioned across different processors.

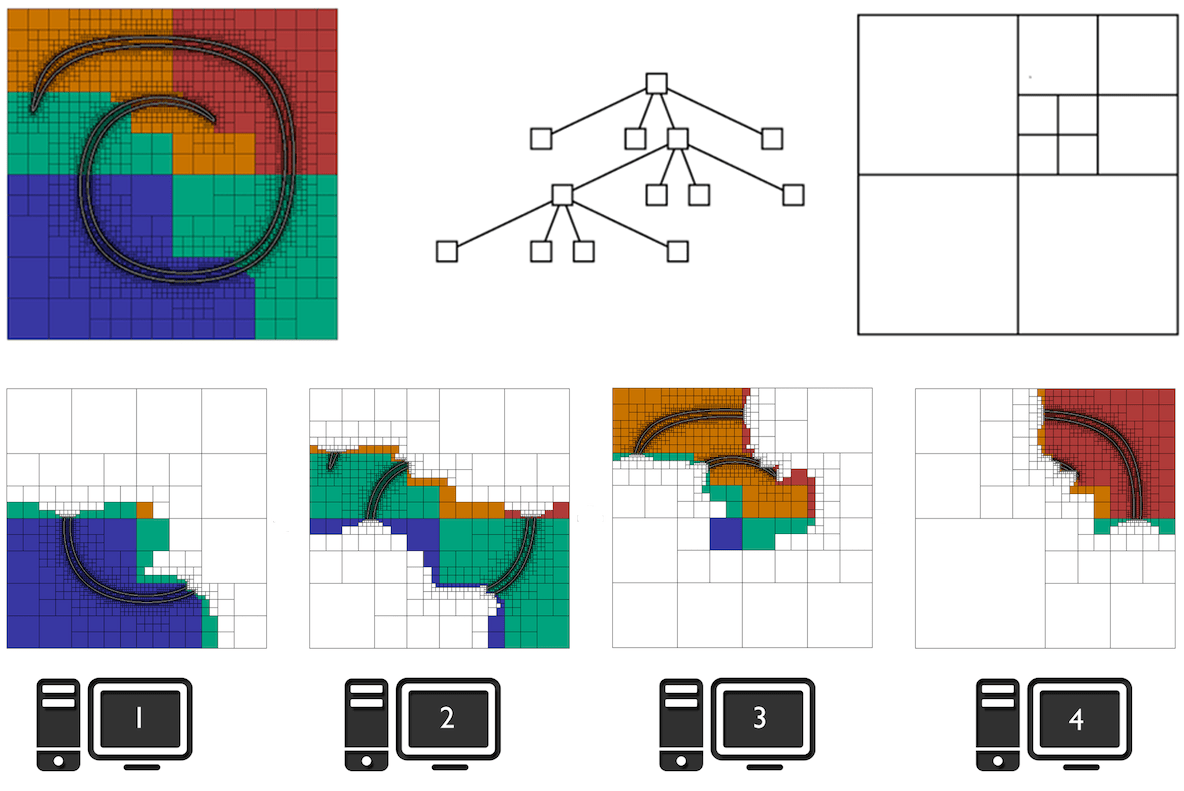
Top: A Quadtree grid, illustrating grid adaptivity and parallel partitioning across four processors as indicated by colors. Bottom: To achieve load balancing, each processor only performs computation on data that is owned locally (in colors) and ignores the rest of the domain (in white). Note how this approach naturally leads to a balanced computation across all processors despite the non-uniform distribution of grid cells.

I have implemented parallel grid-adaptive algorithms using C++ and MPI and successfully applied them to several problems including bimolecular calculations, dendritic crystal growth, and viscous fingering. For more details regarding these algorithms and their applications, please refer to the following papers:

• Mohammad Mirzadeh, Arthur Guittet, Carsten Burstedde, and Frederic Gibou, "Parallel level-set methods on adaptive tree-based grids", Journal of Computational Physics 322, 345-364, 2016.


• Mohammad Mirzadeh and Frederic Gibou, "A conservative discretization of the Poisson–Nernst–Planck equations on adaptive Cartesian grids", Journal of Computational Physics 274, 633-653, 2014.


• Mohammad Mirzadeh, Maxime Theillard, Asdís Helgadöttir, David Boy, Frederic Gibou, "An adaptive, finite difference solver for the nonlinear Poisson-Boltzmann equation with applications to biomolecular computations", Communications in Computational Physics 13, 150-173, 2013.


• Mohammad Mirzadeh, Maxime Theillard, and Frederic Gibou, "A second-order discretization of the nonlinear Poisson–Boltzmann equation over irregular geometries using non-graded adaptive Cartesian grids", Journal of Computational Physics 230, 2125-2140, 2011.

Ion Transport and Electrokinetic Mixing in Random Media

Ion transport and fluid flow in random porous media are relevant to many engineering and biological problems. Both during my PhD and also as a postdoc, I have studied the impact of randomness in porous media on electrokinetics and ion transport. Pore connectivity directly impacts transport pathways and can dramatically affect the kinetics of ion transport. More interestingly, when ion transport is coupled to fluid flow, the electro-osmotic pumping generates non-uniform pressure field inside a medium with random pore connectivity and size distribution. This non-uniform pressure field results in formation of fluid vortices that directly scale with the size of heterogeneities in the medium and can cause strong fluid mixing. For more details, please refer to the following papers:

• Mohammad Mirzadeh, Tingtao Zhou, Mohammad Amin Amooie, Dimitrios Fraggedakis, Todd R. Ferguson, and Martin Z. Bazant, "Vortices of Electro-osmotic Flow in Heterogeneous Porous Media", arXiv preprint arXiv:2003.05974, 2020.


• Mohammad Mirzadeh, Frederic Gibou, and Todd M. Squires, "Enhanced charging kinetics of porous electrodes: surface conduction as a short-circuit mechanism", Physical Review Letters 113, 097701, 2014.

Top: Electrokinetic flows in random porous media generate non-uniform pressure fields which in turn result in formation of vortical structures. The size of these vortices directly correlates with the size of heterogeneity in pore size. Bottom: A rotating electric field generates strong vortices that significantly boost mixing as the electric field strength is increased.

Electrokinetics at Soft and Liquid Interfaces

One of the primary areas of my research is the study of electrokinetic phenomena. Put simply, electrokinetics is the study of mutual interactions and coupling between ionic transport and fluid flow in electrolytes. Because many surfaces contain surface groups which dissociate in water, electrokinetic phenomena are relevant to numerous physical, chemical, and biological systems. Over the past years, I have been studying electrokinetics at liquid interfaces, which have received less attention but often lead to fascinating complex phenomena. An interesting, and unexpected, result is that electrokinetic coupling can impact interfacial instability in a Hele-Shaw cell with dissimilar electrolytes.

It is well-known that viscous fingering occurs when a fluid of lower viscosity displaces a fluid with higher viscosity. However, when an electric field is applied, it is possible to entirely suppress the instability, even for unfavorable viscosity contrast. This remarkable phenomenon is a result of electrokinetic coupling due to non-uniformity in the zeta potential. An ongoing research direction is to extend these ideas to soft interfaces for applications in biological tissues and soft actuators. For more details, please refer to the following papers:

• Tao Gao^‡, Mohammad Mirzadeh^‡, Peng Bai, Kameron M. Conforti, and Martin Z. Bazant, "Active control of viscous fingering using electric fields", Nature Communications 10, 1-8, 2019 (‡ equal contributions)


• Mohammad Mirzadeh and Martin Z. Bazant, "Electrokinetic Control of Viscous Fingering", Physical Review Letters 119, 174501, 2017.

Top: High-resolution simulation of viscous fingering using parallel level-set method. This level of detail is only possible by simultaneous use of grid adaptivity and parallel computing. Bottom: Experimental evidence of EK control of viscous fingering. Here, electrical current flows through a central wire at the center of the Hele-Shaw cell. By applying sufficient current, and in the correct direction, it is possible to suppress or enhance the instability.